historylasas.blogg.se

Of the image entirely, since the samples are guaranteed not to all be close Single sample from each one, we are less likely to miss important features Subdividing the sampling domain into nonoverlapping regions and taking a The key idea behind stratification is that by These regions are commonly called strata, and this sampler is called Into rectangular regions and generates a single sample inside each region.

If you'd like to know more about the theory of Monte Carlo and Latin Hypercube sampling methods, please look at the technical appendices of the manual.The first Sampler implementation that we will introduce subdivides pixel areas Under every combination we've tested, the sample means are much, much closer together with the Latin Hypercube sampling method than with the Monte Carlo method. If you wish, you can change the mean and standard deviation of the input distribution, or even select a completely different distribution to explore. (Select the StandardErrorLHandMC file that matches your version of Select your sample size and number of simulations and click "Run Comparison". The other attached workbooks let you explore the how the distribution of simulated means is different between the Monte Carlo and Latin Hypercube sampling methods.

For convenience, the workbooks already contain graphs, but you can run simulations yourself too. The two attached workbooks show the result of simulating with 720 iterations (72×10), both the Monte Carlo sampling method and the Latin Hypercube method. We chose five integer distributions, each with 72 possibilities, and a Uniform(0:72) continuous distribution with 72 bins. The easiest distributions for seeing the difference are those where all possibilities are equally likely. And when you're performing multiple simulations, their means will be much closer together with Latin Hypercube than with Monte Carlo this is how the Latin Hypercube method makes simulations converge faster than Monte Carlo. This is usually desirable, particularly in when you are performing just one simulation. Therefore, even for modest numbers of iterations, the Latin Hypercube method makes all or nearly all sample means fall within a small fraction of the standard error. This is true for all iterations of a simulation, taken as a group it is usually not true for any particular sub-sequence of iterations. The effect is that each sample (the data of each simulation) is constrained to match the input distribution very closely. Instead, we have stratified random samples.

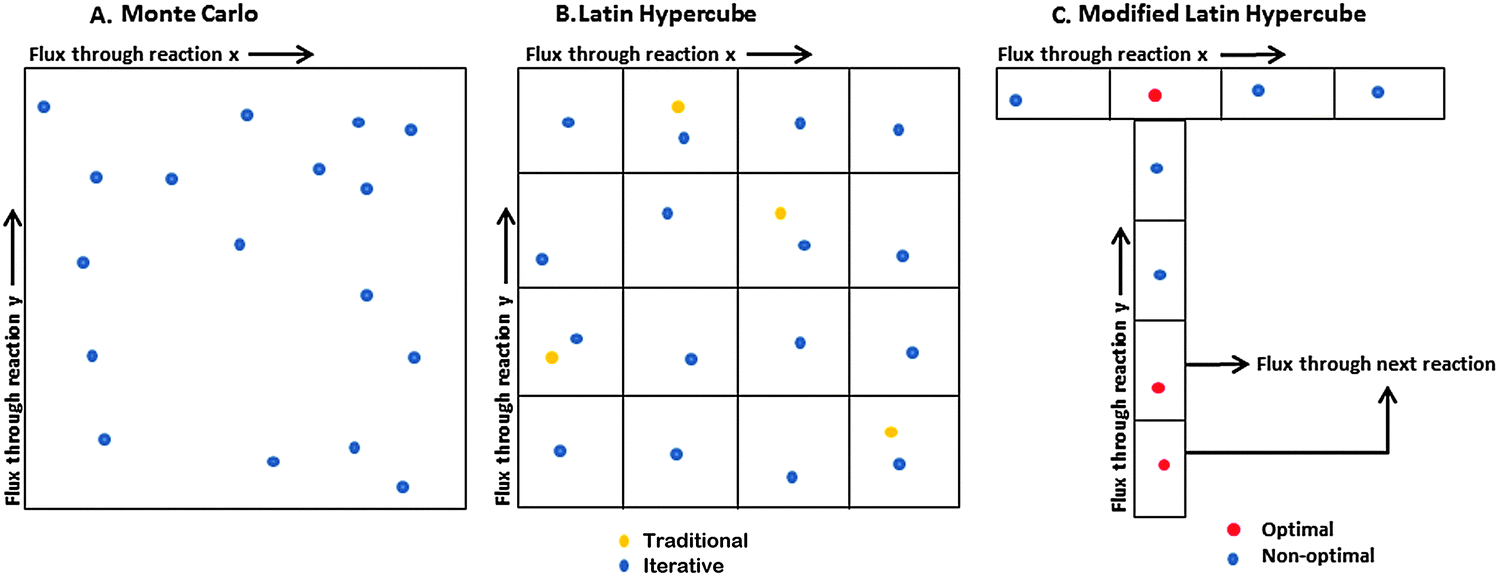
(The number of intervals equals the number of iterations.) We no longer have pure random samples and the CLT no longer applies. In practice, sampling with the Monte Carlo sampling method follows this pattern quite closely.īy contrast, Latin Hypercube sampling stratifies the input probability distributions. With this sampling type, or RISKOptimizer divides the cumulative curve into equal intervals on the cumulative probability scale, then takes a random value from each interval of the input distribution. The CLT tells us that about 68% of sample means should occur within one standard error above or below the distribution mean, and 95% should occur within two standard errors above or below. If you have 100 iterations, the standard error is 20/√100 = 2. For example, with RiskNormal(655,20) the standard deviation is 20.

One SEM is the standard deviation of the input distribution, divided by the square root of the number of iterations per simulation. The Central Limit Theorem of statistics (CLT) answers this question with the concept of the standard error of the mean (SEM). The question naturally arises, how much separation between the sample mean and the distribution mean do we expect? Or, to look at it another way, how likely are we to get a sample mean that's a given distance away from the distribution mean? With enough iterations, Monte Carlo sampling recreates the input distributions through sampling. A problem of clustering, however, arises when a small number of iterations are performed.Įach simulation in or RISKOptimizer represents a random sample from each input distribution. Monte Carlo sampling refers to the traditional technique for using random or pseudo-random numbers to sample from a probability distribution. Monte Carlo sampling techniques are entirely random in principle - that is, any given sample value may fall anywhere within the range of the input distribution.